Criptografia
O básico das tretagem
n3k00n3
O que é Criptografia?
Kriptos = Escondido, oculto; Graphos = Grafia.Ainda não entendi...
Criptografia é o processo de transformar uma informação usando um algoritmo para torná-la ilegível para todos, exceto os que possuem conhecimentos específicos, geralmente referido como uma chave.
E como funciona?
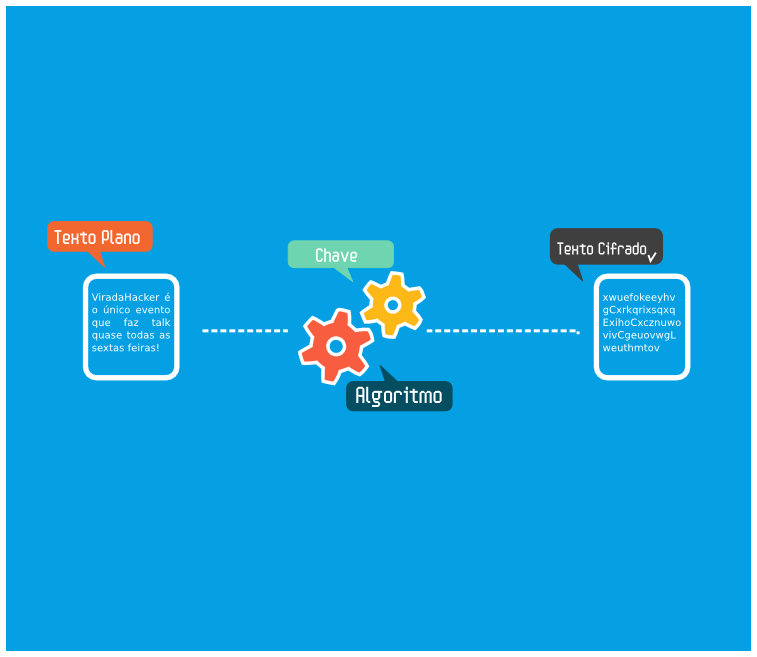
Existem alguns tipos de cripto
- Clássica
- César
- Playfair
- Vigenére
- e muitas outas
- Moderna
- Lúcifer
- DES
- AES
- Mais umas loucas ai
Exemplo 01: Caesar Cipher!
Exemplo 02: Vigenère
Existem dois tipo de cifras
Simétrica
Quando usamos a mesma chave/senha para cifrar uma mensagem e também decifrar essa mensagem
O algoritmo faz a mesma coisa, mas na hora de decifrar ele faz o caminho inverso
Assimétrica
Uso de duas chaves
- Chave Pública
- Chave Privada
RSA
Prepara a caneta ai pra brincar
Primeiro vamos pegar a tabela ascii
A palavra Lampiaosec fica assim em decimal 76 97 109 112 105 97 111 115 101 99
Criando as chaves com número primos
A estratégia para a escolha dos primos é simples: quanto maior melhor. Para se ter uma ideia, a RSA Data Security, que faz a padronização do RSA, recomenda que se utilize chaves de 2048 bits (o que dá um número com 617 dígitos!) se você quiser garantir que sua chave não seja quebrada até 2030. Para nosso exemplo vamos usar primos bem pequenos, que nossas calculadoras conseguem processar. Os primos serão
p = 17, q = 41
Vamos multiplicar eles
n = p * q
n = 17 * 41 = 697
Este n é o tamanho do nosso conjunto. É necessário termos um conjunto finito de valores para que possamos fazer o caminho inverso ao realizado para cifrar nossa mensagem. Podemos, chamar nosso conjunto de Z = 697.
A função Totient
Agora temos que calcular a função totiente, ou φ(x) [pronuncia-se “fi”] de Euler – o matemático, não o filho do vento. O que faz esta função? Eu diria que ela é o cerne do RSA, ela me diz a quantidade de co-primos de um numero que são menores que ele mesmo
Co-primos ou Números primos entre si
Dois números são primos entre si quando o Máximo Divisor Comum (MDC) entre eles é 1.
Calcular a quantidade de co-primos de um número que são menores que ele é um trabalho tão ou mais difícil quanto calcular seus fatores primos… Exceto quando eu já conheço os fatores primos deste número. Para números formados por dois fatores primos ela fica com a seguinte forma:
φ(x) = (p - 1) * (q - 1)
No nosso caso queremos calcular a função totiente do n
φ(n) = (p - 1) * (q - 1)
φ(697) = (17 - 1) * (41 - 1)
φ(697) = 640
Calculando a Chave pública
Devemos escolher um número e em que 1 < e < φ(n), de forma que e seja co-primo de φ(n). Em outras palavras, queremos um e onde o MDC(φ(n), e) = 1, sendo e > 1.
Para encontrar este número podemos ir tentando sequencialmente, iniciando os testes com o número 2:
MDC(640, 2) = 2
MDC(640, 3) = 1
O número 3 atende aos requisitos, mas podemos continuar calculando e usar qualquer co-primo que atenda os requisitos. Para este exemplo vamos usar o número 13.
Chave pública = (n, e)
Chave pública = (697, 13)
Begueza! Descobrimos nossa chave pública! No nosso exemplo ela será os números 697 e 13.
Cifrando a mensagem
Com a chave pública em mãos, é bem simples cifrar uma mensagem. Mas antes temos que fazer uma pausa e entender o que é e como funciona a Aritmética modular e vocês vão perceber que não estou louca quando digo que 13 vezes 9 pode ser 7
Divisão Inteira
Pode parecer estranho, mas é importante termos uma visão bem clara do que é uma divisão inteira para podermos realizar operações modulares. Vejam:
Se y divide x, podemos dizer que
x : y = c
portanto, existe um c tal que
x = c * y + r
onde r é o resto da divisão. Por exemplo:
23 : 7 = c
23 = c * 9 + r
23 = 3 * 7 + 2
E quando o divisor é maior que o dividendo...
5 : 18 = c
5 = c * 18 + r
5 = 0 * 18 + 5
portanto
5 : 18 = 0
5 mod 18 = 5
Aritmética Modular
No dia a dia nós fazemos cálculos em conjuntos numéricos de tamanho infinito. Mas, como poderíamos fazer os mesmos cálculos em um conjunto de tamanho finito? Deixe eu explicar melhor:
13 * 9 = 117
Ok, até agora nada de mais. Mas, e se eu tivesse um conjunto que fosse de 0 a 22?
Vamos chamar o nosso conjunto de Z22.
Z22 = {0, 1, 2, ... , 22}
Temos um problema, 117 não existe no conjunto Z22. Agora, dentro do conjunto Z22,como fazemos aquela conta? Simples, é só pensarmos que o nosso conjunto funciona como um relógio. No relógio, depois das 12 – que é seu valor máximo – ele volta para o 1. Seguindo a lógica, no Z22 quando passarmos de 22 voltamos para o 0. Para realizarmos uma multiplicação modular seguimos os seguintes passos:
- Realizamos a multiplicação comum
- 13 * 9 = 117
- Calculamos o resto da divisão inteira do resultado pelo tamanho do conjunto
- 117 mod 22 = 7
No RSA as operações modulares são extremamente importantes, principalmente a exponenciação. Ela funciona de maneira bem parecida com a multiplicação, vamos ver um exemplo (ainda em Z22):
4 ^ 3 mod 22 = 4 * 4 * 4 mod 22
portanto: 64 mod 22 = 20
E quando a gente vai cifrar mesmo?
Calma jovem padawan!!!
Já sabemos como funciona vamos aplicar a formula!
c = m ^ e mod n
Onde e é a chave pública e m é o valor numérico da letra. No nosso caso vai ser assim.
c = m ^ 13 mod 697
| Letra | Formula | Resultado |
|---|---|---|
| A | 468 ^ 197 mod 697 | 468 |
| a | 97 ^ 13 mod 697 | 252 |
| m | 109 ^ 13 mod 697 | 465 |
| ... | ... | ... |
| c | 99 ^ 13 mod 697 | 22 |
Nosso texto cifrado!
468 252 465 198 318 252 110 676 220 222
Massa! e como é que eu faço pra reverter?
Só rezar! :) to de brinks!
Vamos direto ao ponto porque já está chato...eu sei =^.^=
Vamos recaptular algumas coisas
P = 17, Q = 41, N = 697, Z = 640, E = 13
Achando o nosso d
Precisamos achar um número que satisfaça essa expressão(d*e) mod Z = 1
197 satisfaz pois d = (197 * 13) % 640 é igual a 1
Para recuperar a mensagem, precisamos executar a expressão M = Cd mod n, ou seja, M = C ^ 197 mod 697
| Letra | Formula | Resultado |
|---|---|---|
| 468 ^ 197 mod 697 | 76 | |
| \xFC | 252 ** 197 % 697 | 97 |
| 465 ^ 197 mod 697 | 109 | |
| ... | ... | ... |
| \x16 | 22 ^ 13 mod 697 | 99 |
Nosso texto decifrado!
76 97 109 112 105 97 111 115 101 99
Porque usar Criptografia?
- Integridade da Mensagem
- Autenticidade da Mensagem
Vamos ao exemplo!
- Autenticando e criptografando
- Emma escreve uma mensagem e criptografa com sua chave privada.
- Em seguida ela criptografa com a mensagem com a chave pública da N3k00n3.
- Emma envia essa mensagem para n3k00n3
- n3k00n3 recebe a msg e então usa a sua chave priva para descriptografar a msg
- n3k00n3 usa a chave pública da Emma para descriptografar
Ela sabe que só Emma poderia usar a chave privada dela
Obs: Emma pode ter sido hackeada e ter perdido a sua chave privada :) (sem paraoia)
Existem várias ferraments como PGP e GnuPG
O lampiaosec está fazendo o virgulino
O virgulino além de encriptar/descriptografar ele Esteganografra
